Machine Learning - Basics of Data Mining
There are several problems which make data preprocessing necessary.
- Data Format
This can be very difficult as data representation can differ stronly and conversion between different representations can not be generalized but has to be solved problem specific - Outliers and Missing Values
Outliers
The problem is that outliers can spoil our statisitcs. Taking the mean of a small dataset with extreme outliers will lead to a strong shift –> consider replacing the mean by the median.
Causes for outliers:
- Technical errors / errors by measurement
- Unexpected “true” effect
- data with high variation - outliers are a natural part of the distribution
Outlier detection
When an outlier was detected, we can either remove it or we replace it. To detect an outlier first we have to define what is regular. Most often we assume the data to be normally distributed. For multivariate data, we can first cluster the data and then assume a normal distribution for each cluster.
z-test
Outliers of univariate distributions can be detected from z-values: \(z_i = \vert x_i - \mu\vert / \sigma\). Here \(z_i\) is a measure of the distance of \(x_i\) from the mean \(\mu\) in terms of the standart deviation \(\sigma\). Commonly, datapoints with \(z_i > 3\) are considered outliers.
Improvement:
Use the median instead of the mean to counter the outliers influence and increase the treshold to 3.5!
Rosner test
The idea is to iteratively remove outliers until z-testing doesn’t result in any more outliers.
while True:
calculate mean or median and standart deviation
find data-point x_i with largest z_i
if z_i is an outlier:
remove x_i
else:
break
Once we detected our outliers we have to handle them. One option is to simply remove them. This results in information loss and therefore we should consider to replace or weight the outliers instead.
Missing values
Missing values pose a major problem as they can make most of our data unusable if no measure is taken.
Imagine that a datapoint consists of 100 elements. If the probability that a value is missing is \(p=2\%\) then the probability that the vector is complete and therefore usable is \((1 - p)^{100} = 13\%\). If we don’t do anything we wont be able to use \(87\%\) of the data!
Idea 1 Replace missing values by the mean or median from the rest of the data set.
Idea 2 Estimate a model to predict missing values, f.e. linear regression.
\(y' = y_s x + y_{0}\) \(x' = x_s y + x_{0}\)
\(y_s = C_{xy}/C_{xx}\) \(x_s = C_{xy}/C_{yy}\)
\(y_0 = \mu_y - y_s\mu_x\) \(x_0 = \mu_x - x_s\mu_y\)
\(C_{xy}\) is the covariance of x and y and is \(C_{xy} = \sum_{i=1...n}(x_i - \mu_x)*(y_i - \mu_y)\)
We use two different regression lines to minimize the error of x and y independitly.
\(y'\) minimizes \(\sum_{i=1...n}(y_i - y'_{x_i})\)
\(x'\) minimizes \(\sum_{i=1...n}(x_i - x'_{y_i})\)
Idea 3 Estimate the data distribution \(P(x,y)\) (assuming a nomal distribution \(P(x,y) = N(\vec{\mu}, C))\), C being the covariance matrix.
The problem when estimating \(P(x,y)\) is that we can only use the complete data-points and therefore loose all the information contained in the uncomplete data-points.
Idea 4 Usage of the Expectation Maximization (EM) algorithm to estimate P(X,Y) by using both complete and partial data-points in an iterative manner.
Defenitions:
x denote all specified data (complete and partial data-points)
h all “hidden” (missing values)
\(\theta\) all parameters of the chosen distribution (such as mean and variances for a Gaussian)
The probability of the known values \(x\) depends on the distribution (specified by \(\theta\)) \(P(x\vert\theta)\) . The probability of the hidden values \(h\) depends on the distribution (\(\theta\)) and on the data \(x\) so \(P(h \vert x, \theta)\).
Thus the total distribution is defined as \(P(x, h \vert\theta) = P(h\vert x, \theta) * P(x\vert\theta)\)
The likelihood of parameters \(\theta\) as a function of \(x\) and \(h\) is \(L(\theta; x,h) = P(x, h\vert \theta)\)
For convenience, we consider the log-likelihood instead: \(I(\theta) = \log L(\theta; x,h) = \log P(h \vert x, \theta) + \log P(x\vert\theta)\)
We want the parameters \(\theta\) that maximize the log-likelihood \(I(\theta)\).
We get the \(l(\theta) = \log P(x,h,\theta) = \log P(h \vert x, \theta) + \log P(x \vert \theta)\) by:
- removing the hidden values h by “avering out” to obtain an averaged \(<l(0)>_h\)
- to do so, we need the probability \(P(h \vert x, \theta)\), here we need an estimate \(\theta_t\) fot the real \(\theta\)
We use an iterative approach to improve our estimate \(\theta_t\) (M-step) and averaring over h using the obtained \(\theta_t\) (E-step). \theta _t will converge to a local maximum \(\theta^\star\) of l (hopefully close to \(\theta\))
Thus we maximize the averaged likelihood \(Q(\theta, \theta_t) = <l(\theta)>_h = \int P(h\vert x,\theta_t)*\log P(h\vert x, \theta)\mathrm{d}h + \log P(x\vert\theta)\) so we have traded the h-dependence of l for a \(\theta_t\)-dependence of Q.
choose function to approximate P(x,y | theta) woth parameters theta
choose start values theta_t
t = 0 # step counter
while True:
# E-step
Q_theta_theta_t = integral function from above
# M-step
theta_t = argmax_theta(Q_theta_theta_t)
t += 1
if Q_theta_theta_t meets convergence condition:
break
EM-Algorithm 2D-Visualization
…..
Distance function
Theoretically our goal is to get relatations between data on the sematic level, in particular, similarity / dissimilarity. In practice we try to approximate semantic relations with numerical measures, in particular, distance functions/metrics.
A distance function or metric d must obey the following conditions which are reasonable for geometric distances (i, j and k are locations)
- Symmetry: \(d_{ij} = d_{ji}\)
- Coincidence axiom: \(d_{ij} = 0 \Leftrightarrow i=j\)
- Triangle equation: \(d_{ik} + d{kj} \geq d_{ij}\)
Note the axioms imply d_{ij} \geq 0
Remark In mathematics, the term distance function is used only when these acioms are fulfilled but in ML, distance function will often be used like dissimilarity function and may be applied to quantities that do not match the axioms. To make it crystal clear you mean a distance function fulfilling the axioms, use the term metric.
Distance matrix:
For a data set \(\{\vec{x_1} ... \vec{x_n}\}\) all information about distances is assembled in the distance matrix
\(D =
\begin{bmatrix}
d_{11} & ... & d_{1n} \\
... & & ... \\
d_{n1} & ... & d_{nn}
\end{bmatrix}\)
Similarity matrix:
Distance calculation is motivated from geometric distances but in ML, distances are more broadly used to express similarity. Similarities of data may be represented by a matrix as well as as distances.
When simlarities are not computed from features of the data, but assigned explicitly from ither sources (e.g., human insight), similarities may become particularly “non-geometrix”.
Distance functions:
Some common distances for \(\vec{x}, \vec{y} \in \Re^L\) are:
- Euclidean distance: \(d(\vec{x}, \vec{y}) = \vert\vert\vec{x}, \vec{y}\vert\vert = (\sum_{i=1...L}(x_i - y_i)^2)^{1/2}\)
- simple and frequently used measure
- no individual weighting of components
- Pearson distance: \(d(\vec{x}, \vec{y}) = \vert\vert\vec{x}, \vec{y}\vert\vert = \sum_{i=1...L}(x_i - y_i)/\sigma_i\) with standard deviations \(\sigma_i\)
- weighted dimensions on their variation from the mean
- also called “normalized euclidean distance” or “\(\chi^2\)-distance”
- Mahalanobis distance: \(d(\vec{x}, \vec{y}) = ((\vec{x}-\vec{y})^T C^{-1}(\vec{x} - \vec{y})) ^ {1/2}\)
- distances scaled using the covariance matrix C
- scale and translation invariant
- if C is unit matrix: euclidean distance
- points of equal Mahalanobis distance to a center form an ellipsoid
- Manhatten distance: \(d(\vec{x}, \vec{y}) = \sum_{i=1...L} \vert\vec{x_i}-\vec{y_i}\vert\)
- Chebyshev distance: \(d(\vec{x}, \vec{y}) = max_{i=1...L} \vert\vec{x_i}-\vec{y_i}\vert\)
p-norm:
Generalization: $$d(\vec{x}, \vec{y}) = (\sum_{i=1…L}\vert x_i - y_i\vert ^p)^{1/p}
Special cases:
- \(p = 1\): \(d(\vec(x), \vec(y)) = \sum_{i=1...L}\vert vec{x_i} - vec{y_i}\vert\) (city-block)
- \(p = 2\): \(d(\vec(x), \vec(y)) = (\sum_{i=1...L}(x_i - y_i)^2)^{1/2}\) (euclidean)
- \(p \rightarrow \infty\): \(d(\vec(x), \vec(y)) = max_{i=1...L} \vert x_i - y_i \vert\) (maximum)
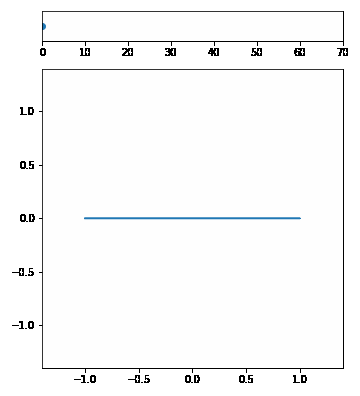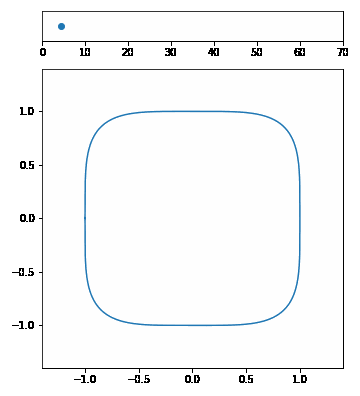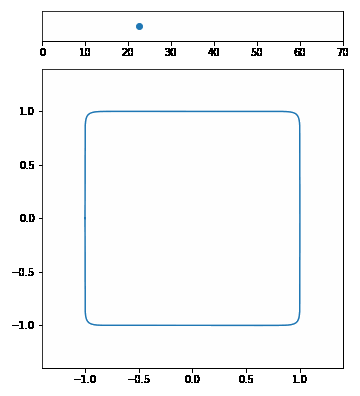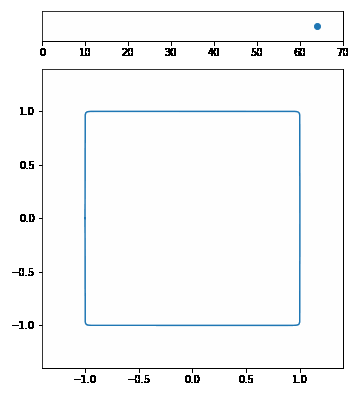
| The p-Norm is defined by $$|\vec{x}|p = (\sum{i=1}^n | x_i | ^p)^{1/p}$$. | ||||
| We want to visualize a unit circle in different p-Norms so \(\vec{x}\) is 2-dimensional. Our p-Norm formula can therefore be written as $$|(x_1, x_2)|_p = ( | x_1 | ^p + | x_2 | ^p)^{1/p}$$. | ||
| To draw the unit circle we simply have to solve \(|(x_1, x_2)| = 1\). $$1 = ( | x_1 | ^p + | x_2 | ^p)^{1/p}\(,\)x_2 = \pm (1 - | x_1 | ^p)^{1/p}$$ |
Embeddings
We need to use a embedding if our data uses a different topology than \(\Re^n\). One example for a other topology are angular attributes:
\(\vert\vert 10^• - 30^•\vert\vert = 20^•\)
\(\vert\vert 0^• - 359^•\vert\vert = 359^•\)\
Nominal Scales:
We can map nominal attribute values to real values:
\((low, mwdium, high) \rightarrow (1,2,3)\) makes sense but
\((stone, wood, metal) \rightarrow (1,2,3)\) implies an order that is nopt there.
Solution: \((stone, wood, metal) \rightarrow ((1,0,0)^T, (0,1,0)^T, (0,0,1)^T)\)
Problem: For a large number n of attribute values, doimensionality becomes too high.
Solution: Choose normalized random vectors \(v_i\in \Re^m, i=1...n, 1<<m<<n\) instead. Vectors drawn at random from a space of high dimension tend to be close to orthogonal (why?)
Binary scales:
For binary attributes (e.g. small/big, yes/no) use te Jaccard index J as a similarity measure which is defined for sets A and B:
\(J(A, B) = \vert A \cap B \vert / \vert A \cup B \vert\) ((# common elements) / (# all elements))
Jaccard distance function: \(J_d(A, B) = 1 - J(A, B)\)